
三角関数では最大値と最小値を求める問題も頻繁に出題されます
今回は最大値と最小値を求める問題の中でも、\(θ\)の範囲が指定されていない問題の解き方を説明していきます
※範囲が決まっていない三角関数の最大値と最小値のその他の問題はこちら

目次
\(θ\)の範囲が決められていても決められていなくても、考え方は同じ
三角関数の最大値と最小値を求める問題のほとんどは、問題文の中に\((0≦θ<π)\)や\((0≦θ<2π)\)などと書かれています
つまり、これらの問題は\(θ\)の範囲が決められていて、決められた\(θ\)の範囲の中にある最も大きい値と最も小さい値がその問題の答えとなります
では、範囲指定のない三角関数の最大値と最小値はどうやったら求められるでしょうか
範囲が決まっていない三角関数は、その関数の全ての値の中で最も大きい値と最も小さい値が答えとなります
難しそうに思いますが、\(θ\)の範囲が決まっていても決まっていなくても、問題の考え方に違いはありません
それどころか、実は\(θ\)の範囲指定がない問題のほうが、範囲指定がある問題よりも簡単に答えが求められます
では、以下の例題を使って三角関数の最大値と最小値を求める問題の解き方を説明していきます
【例題】\(y=4sinθ+3cosθ\)の最大値と最小値を求めよ
【例題】\(y=4sinθ+3cosθ\)の最大値と最小値を求めよ

【例題】\(y=4sinθ+3cosθ\)の最大値と最小値を求めよ
※2倍角の公式を使った三角関数の最大値と最小値の求め方はこちら
※「2次式で表して\(t\)とおく」方法を使った三角関数の最大値と最小値の求め方はこちら
三角関数の合成から始める
まず、問題の式は、\(sin\)と\(cos\)が混在しているので、三角関数の合成を使って、\(sin\)だけの式にします
三角関数の合成は、\(sin\)\(θ\)と\(cos\)\(θ\)や\(sin\)\(3θ\)と\(cos\)\(3θ\)など、角の大きさが等しい\(sin\)と\(cos\)が出てきた時に使えます
この問題は、\(4sin\)\(θ\)と\(3cos\)\(θ\)なので、三角関数の合成を使って\(sin\)だけの式に変形して解いていきます
三角関数の合成
実際に\(y=4sinθ+3cosθ\)を合成していきます
三角関数の合成の方法がわからない場合はこちらを確認してください
\[\begin{eqnarray}\displaystyle\\y&=&4sinθ+3cosθ\\y&=&\sqrt{4^2+3^2}sin(θ+α)\\y&=&\sqrt{25}sin(θ+α)\\y&=&5sin(θ+α)\end{eqnarray}\]ただし、\(sinα=\frac{3}{5}\),\(cosα=\frac{4}{5}\)
これで、\(y=4sinθ+3cosθ\)は\(y=5sin(θ+α)\)に変形することができました
\(y=5sin(θ+α)\)のグラフをイメージしてみよう
範囲のない2次関数の最大値と最小値を考えるとき、グラフを書き、グラフ上で最も大きい値や最も小さい値を見つけて答えとしていました
範囲のない三角関数の最大値と最小値も、この2次関数の最大値と最小値と同様にして考えることができます
では、\(y=5sin(θ+α)\)のグラフを考えてみましょう
\(y=5sin(θ+α)\)のグラフは、\(y=sinθ\)のグラフを\(x\)軸方向に\(-α\)だけ平行移動し、\(y\)軸方向に5倍したものです
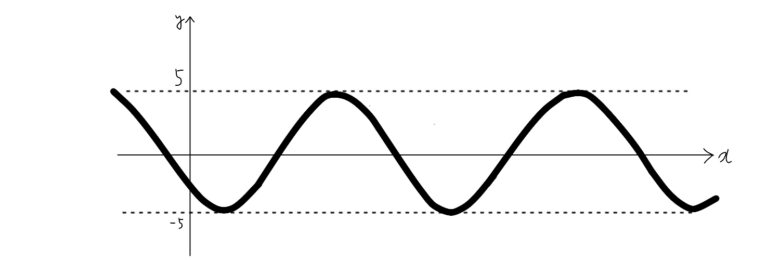
グラフがイメージできたら答えはすぐにわかります
\(y=4sinθ+3cosθ\)の最大値と最小値
\(y=4sinθ+3cosθ\)のグラフより、この式の\(y\)の値は\(-5≦y≦5\)の間で変化しています
つまり、\(y\)の値はどんなに小さくても\(-5\)で、また、どんなに大きくても\(+5\)となります
よって、この問題の答えは
最大値…\(5\)、最小値…\(-5\)
※範囲が決まっていない三角関数の最大値と最小値のその他の問題はこちら
