
碁盤の目の最短経路に関する場合の数や確率の問題は、同じものを含む順列を使うと答えを求められます
しかし、確率の問題の中には同じものを含む順列ではなく「反復試行の確率」を使って解くものがあります
同じ碁盤の目の最短経路に関する確率の問題なのに、なぜ解き方が違うのでしょうか
その理由は、問題文の中の「ある一言」にあります
では、反復試行の確率を使って解く最短経路の問題を、例題を使って説明していきます
目次
碁盤の目の道路の最短経路の問題
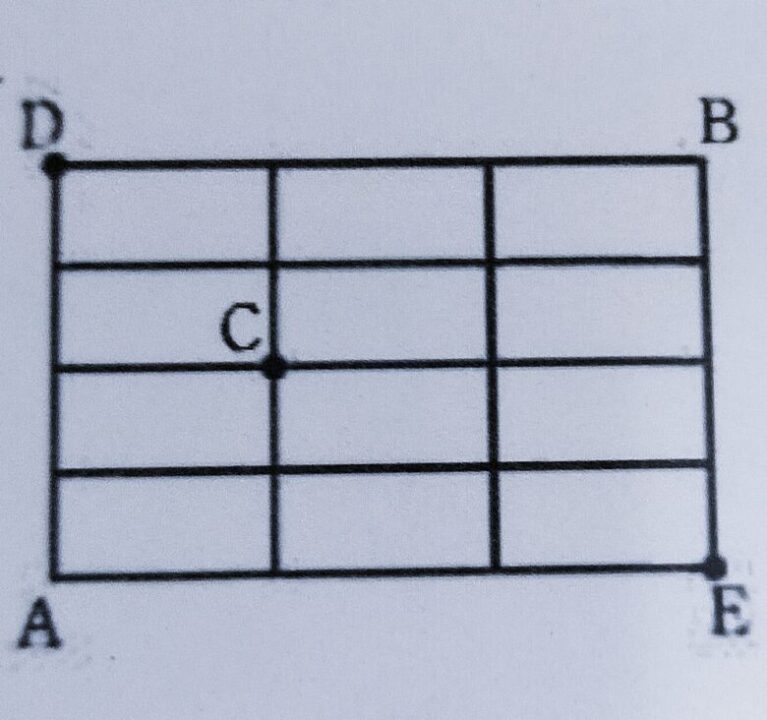
【例題】図のような碁盤の目の道路がある。いま、A地点にいる人が、B地点まで最短距離で向かうとする。ただし、2通りの選び方のある交差点では、どちらを選ぶかは\(\frac{1}{2}\)の確率とする。このとき、C地点を通る確率を求めよ。

よくある間違い
この問題のよくある間違いは、同じものを含む順列を使って解いてしまうことです
以下に間違いを書きます
全ての道順が何通りあるか計算すると、\(\frac{7!}{3!4!}=35\)
Cを通る道順が何通りあるか計算すると、\(\frac{3!}{1!2!}×\frac{4!}{2!2!}=18\)
よってAからCを通ってBまで行く確率は\(\frac{18}{35}\)
以上がよくある間違いです
実はこの問題は「同じものを含む順列」ではなく、「反復試行の確率」を使って解かなければなりません
「反復試行の確率」かどうかを見分ける「ある一言」とは?
この問題は、問題文の中に「ある一言」が書かれているため、「同じものを含む順列」ではなく、「反復試行の確率」を使って解くことになります
その「ある一言」とは、「交差点では、どちらを選ぶかは\(\frac{1}{2}\)の確率とする」です
一言といいながら長いですね…
つまり、分岐点で進む方向を選ぶ確率が問題文の中に書かれていれば「反復試行の確率」を使い、書かれていなければ「同じものを含む順列」を使って解くと覚えてください
この「ある一言」の書き方が問題によって色々とあるので、たくさん類題を解いてテストや入試に備えてください
共通テストなどでもたまに出題されてますので、過去問もぜひ解いてみましょう
「反復試行の確率」を使った正しい解き方
反復試行の確率の公式
\(_nC_rp^r(1-p)^{n-r}\)
AからCに行くには、どの道を通っても必ず「交差点が3か所」あり、3か所のうちどこかで「上を2回」、そして別のどこかで「右を1回」選ばなければなりません
3か所のうちどこか2か所で上を選ぶと、残り1か所は自動的に右と決まるので、反復試行の確率の公式の前半、組み合わせの部分は\(_3C_2\)となります
反復試行の確率の公式の後半は、「上を2回選ぶ確率」が\(\frac{1}{2}×\frac{1}{2}\)、右を1回選ぶ確率」が\(\frac{1}{2}\)となるので、まとめると\((\frac{1}{2})^2×(\frac{1}{2})^1\)となります
式をまとめると、\(_3C_2(\frac{1}{2})^2(\frac{1}{2})\)となり、これを計算すると
\[\begin{eqnarray}\displaystyle_3C_2(\frac{1}{2})^2(\frac{1}{2})&=&\frac{3×2}{2×1}×\frac{1}{4}×\frac{1}{2}\\&=&3×\frac{1}{8}\\&=&\frac{3}{8}\end{eqnarray}\]
よって、この問題の正しい答えは\(\frac{3}{8}\)となります
※式の成り立ちがわかりにくい人は下の樹形図も参考にしてください
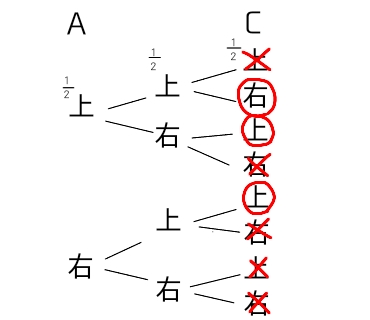
上上右といく確率が\(\frac{1×1×1}{2×2×2}\)
上右上といく確率が\(\frac{1×1×1}{2×2×2}\)
右上上といく確率が\(\frac{1×1×1}{2×2×2}\)
合わせると\(\frac{3}{8}\)通り

同じものを含む順列では間違いとなる理由
分岐点で進む方向を選ぶ確率が問題文の中に書かれているとき、同じものを含む順列で解くとなぜ間違いになるのでしょうか
その理由は、全35通りある道順で、それぞれの道を通る確率が全て同じではないからです
実はコイン投げと同じ理論
問題文のように「2通りの選び方のある交差点では、どちらを選ぶかは\(\frac{1}{2}\)の確率とする。」と書かれているからわかりにくいのです
交差点でコイン投げを3回し、表が出たら上に、裏が出たら右に進むと考えてみてください
すると3回投げ終えた時にいる場所は下の図の赤字の位置になります
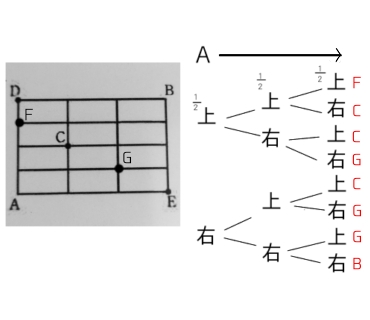
上の図より、Fにいる確率は\(\frac{1}{8}\)、Cにいる確率は(\frac{3}{8})、Gにいる確率は\(\frac{3}{8}\)、Bにいる確率は(\frac{1}{8})なので、ある地点を通る確率は同じにはなりません
分岐点で進む方向を選ぶ確率が上と右で違う場合を想像してみよう
ここまでの説明でも何が違うのかまだわからないと感じる人もいると思います
そんな時は、分岐点で進む方向を選ぶ確率が上と右で違う問題を想像してください
例えば、上を選ぶ確率が\(\frac{3}{4}\)、右を選ぶ確率が\(\frac{1}{4}\)とすると、明らかに上の方の道を通る可能性の方が高くなりますよね
よって、それぞれの道を通る確率が全て同じにはならないため、「反復試行の確率」で解かなければならないのです
分岐点で進む方向を選ぶ確率が書かれていない場合は、ただ単純に「地点Cを通るか通らないか」だけを判断するので、「同じものを含む順列」で解くことになります
