
立方体の6面を6色で塗り分ける問題などは簡単な問題集でもよく出題されていますが、正四面体の4面を塗り分ける問題は少し珍しいかもしれません
今回はそんな少し珍しい問題、「正四面体の4面を赤,青,黄,緑の4色で塗り分ける方法は何通りあるか」を解説していきます
目次
展開図を回転させたら同じになるものは1通りと考える
正四面体を塗り分ける問題も立方体を塗り分ける問題と同じで回転させたら同じ色使いになるものは1通りと考えます
したがって、下記の図の配色はすべて同じと考えられ、1通りとされます
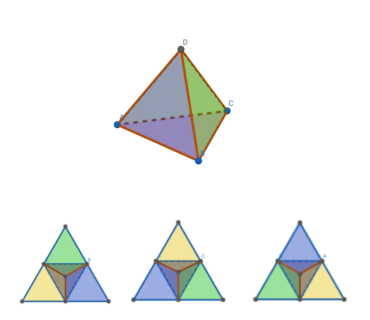
ゆえに、展開図の真ん中の三角形の色を決めると、周りの3つの三角形の配色は円順列で求められます
答えを導く式は以下になります
\begin{align}&(3-1)!\\=&2✕1\\=&2\\&答え…2通り\end{align}

「真ん中の色は4色から選べるので4をかけ算する」必要はありません
「真ん中の色は4色から選べるので4をかけ算する」必要はありません
なぜなら、展開図を回転させたものだけでなく、「正四面体そのものを回転させて同じ配色になったものは1通り」と考えるからです
つまり、以下の4つの展開図は組み立てて回転させると同じになるので1 通りと考えます
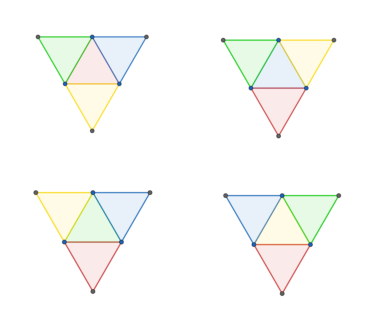
以上より、考えられる塗り方は以下の2つになります
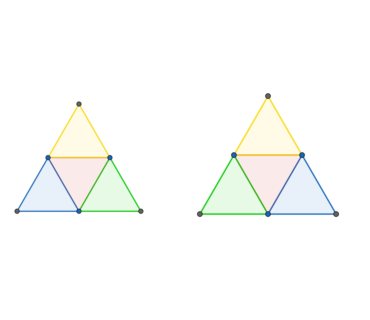
したがって、正四面体の4面を赤,青,黄,緑の4色で塗り分ける方法は2通りです

おまけ:12色の中から4色を使って正四面体を塗り分ける方法は何通りあるでしょうか
使う4色さえ決まってしまえば、その4色を使った塗り方は2通りとなります
つまり、使う色の組み合わせが何通りかわかれば、それを2倍するだけで答えが求められます
よって、まずは組み合わせ\(C\)を使い、12色から4色選ぶと何通りになるか考えます
\begin{align}&_{12}C_4\\=&\frac{12✕11✕10✕9}{4✕3✕2✕1}\\=&495\end{align}
この495通り全てに2パターンの塗り方があるため、\begin{align}&495✕2\\=&990\end{align}
ゆえに、答えは990通りとなります