
対数関数の最大・最小を求める問題もテストによく出題されますね
ほとんどの問題は底が1より大きく、真数の部分が2次式になっているので、平方完成して頂点を求めれば、最大値または最小値が求められます
では底が1より小さいときの最大値・最小値はどうなるのでしょうか?
目次
底が1より小さい場合の最小値・最小値
結論から先に述べると、底が1より小さい場合は、真数が最大のとき\(y\)の値が最小となり、真数が最小のとき\(y\)の値が最大となります
底が1より大きい場合は、真数が最大のとき\(y\)の値が最大、真数が最小のとき\(y\)の値が最小となるため、底が1より小さい場合は、最大値・最小値の値が逆になっていると言えます

底が1より小さい場合、最大・最小が逆になる理由
グラフの対称移動を思い出してください
数Ⅰの2次関数で、\(y=f_{(x)}\)と\(y=-f_{(x)}\)は\(x\)軸に関して対称なグラフであると学習しました
また、中学生の頃から\(y=x\)と\(y=-x\)は\(x\)軸に関して対称なグラフであり、\(y=x^2\)と\(y=-x^2\)も\(x\)軸に関して対称なグラフであると学習、そして、この関係性は対数関数のグラフにも当てはまります
\(y=\log_{\frac{1}{4}}x\)を例とすると、\(y=\log_{4}x\)と\(y=-(\log_{4}x)\)は\(x\)軸に関して対称なグラフであり、\(y=\log_{\frac{1}{4}}x\)は\(y=-(\log_{4}x)\)と底を変換できるため、\(y=\log_{\frac{1}{4}}x\)と\(y=\log_{4}x\)は\(x\)軸に関して対称なグラフであるといえます
したがって、底が1より小さい場合は、真数が大きくなるほど\(y\)の値が小さくなるため、真数が最小のとき\(y\)が最大となります
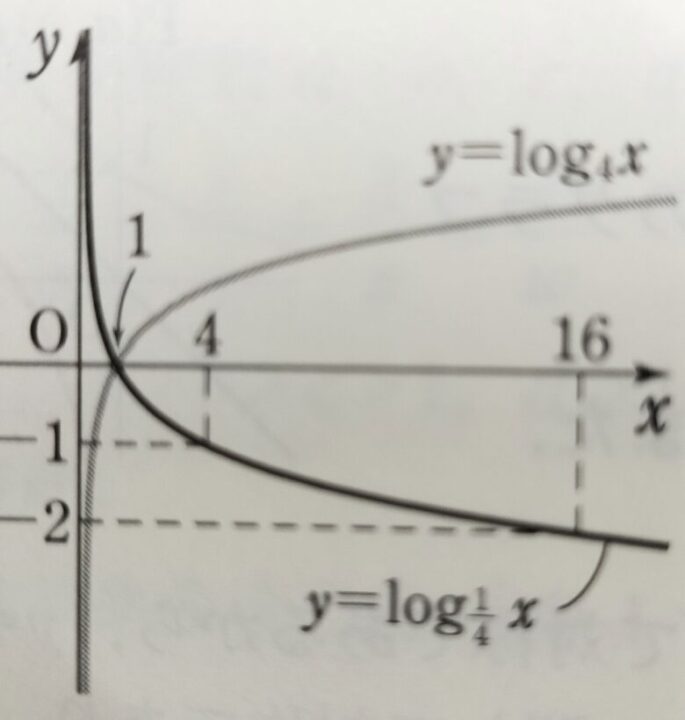
\(y=\log_{\frac{1}{3}}x+\log_{\frac{1}{3}}(6-x)\)の最小値はどうやって求める?
この問題は底が1より小さいので、真数が最大のとき\(y\)の値が最小になります
真数の最大値を見つけるために、対数の性質や平方完成を利用して式を変形し、真数が最大のときの\(y\)の値を計算すれば答えとなります
まず、真数の条件を確認しておきます
真数は正であるから、\(x>0\)かつ\(6-x>0\)より、\(0<x<6\)
次に、対数の性質を使って式を変形します\begin{align}y&=\log_{\frac{1}{3}}x+\log_{\frac{1}{3}}(6-x)\\y&=\log_{\frac{1}{3}}x(6-x)\\y&=log_{\frac{1}{3}}(-x^2+6x)\end{align}
そして、真数の部分が2次関数になっているため、平方完成を行い、\(0<x<6\)の範囲で真数が最大となる\(x\)の値を求めます
平方完成\begin{align}y&=log_{\frac{1}{3}}(-x^2+6x)\\y&=log_{\frac{1}{3}}\{-(x-3)^2+9\}\end{align}よって、\(0<x<6\)の範囲では、\(x=3\)のとき真数の最大値が\(9\)となります
※\(x\)の値と、そのときの真数\[y=log_{\frac{1}{3}}\{-(x-3)^2+9\}\]\begin{array}{c|cc} x&1&2&3&4&5\\ \hline真数&5&8&9&8&5\end{array}
最後に、真数が\(9\)のときの\(y\)の値を計算します
底が1より小さいので真数が\(9\)のときの\(y\)の値が最小値となります\begin{align}y&=log_{\frac{1}{3}}9\\y&=log_{\frac{1}{3}}\left(\frac{1}{9}\right)^{-1}\\y&=log_{\frac{1}{3}}\left(\frac{1}{3}\right)^{-2}\\y&=-2\end{align}
よって\(y\)は\(x=3\)で最小値\(-2\)をとる
対数関数の最大値・最小値のその他の問題
相加・相乗平均の使い方は?2つの正の数の和の最小値をもとめよう!\[a=log_2x,b=log_8yとする\\a+3b=6のとき\\x+yの最小値を求めよ\]
