同じものを含む円順と同じものを含む数珠順列−白玉4個・黒玉3個・赤玉1個を円形に並べる方法と紐を通して輪を作る方法−

いくつかのものを円形に並べる場合は円順列、数珠状にする場合は数珠順列と覚えてる人は多いでしょう

しかし、この問題を円順列と数珠順列の公式にただ当てはめると間違いになります

なぜ間違いになるのでしょうか

その理由は、「異なるいくつかのもの」を並べる場合が円順列、「異なるいくつかのもの」を数珠状にする場合が数珠順列、だからです

公式は「異なるもの」を並べる場合のみ、そのまま使えます

この問題は、この問題は、白玉4個・黒玉3個・赤玉1個を並べるので、「異なるもの」ではなく、「同じものを含む円順列」と「同じものを含む数珠順列」と考える必要があります

白玉4個・黒玉3個・赤玉1個を円形に並べる

考え方はいくつかありますが、今回は最も一般的で、教科書や参考書に書いてある「赤玉を固定して、残り7個を並べ替える」方法で説明していきます

どの参考書を見ても「固定する玉は赤玉」と書いてあるけど、固定するのはなぜ赤玉なの？

実は、固定する玉は赤色でなくても答えを求めることは可能です
ただし、赤玉以外を固定すると、同じ色の玉が複数存在するため、計算がとても複雑で面倒になります

ひとつしかない赤玉を固定し、簡単に答えを求めましょう

赤玉を固定すると、残りの玉を並べる場所は以下の図の通りになります

綺麗な円形だとわかりにくいので、わざと偏った輪の形にしてみました

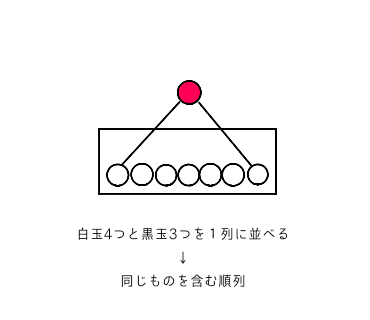
赤玉の下にある7カ所に白玉4つと黒玉3つを当てはめて１列に並べると、白玉4つ・黒玉3つ・赤玉1つを円形に並べたときの答えになります

つまり、計算方法は白玉4つと黒玉3つを並べる「同じものを含む順列」で求められます

白玉4つと黒玉3つを並べる「同じものを含む順列」で求められるとわかったので実際に計算していきましょう

\begin{align}&\frac{7!}{4!3!}\\=&\frac{7・6・5・4・3・2・1}{4・3・2・1✕3・2・1}\\=&35\end{align}

答え35通り

この問題を「紐を通して輪にするから数珠順列だ」という考え方をした場合、ほとんど正しいといえますが、完全な正解とは言えません

なぜなら、この問題は、同じ色の玉が複数ある「同じものを含む数珠順列」であり、普通の数珠順列で計算すると間違いになるからです

「円形に並べる」という問題は、特に明文化されていなくても、玉などの小物は台の上に並べることになります

つまり、ただひとつひとつがバラバラに並んでいるため、全体を持ち上げたりひっくり返したりすることはできません

しかし、並べた玉に紐をつけて輪にすると持ち上げたりひっくり返したりすることができます

この持ち上げたりひっくり返したりすることができる状態のことを「数珠順列」といいます

そして、数珠順列では「裏返してできる並び方は表と同じもの」と考えるため、円形に並べるときと比べて同じものが2つある状態になります

ここでいう「裏返してできる並び方」とは、以下の図でいう線対称の関係になっているものです

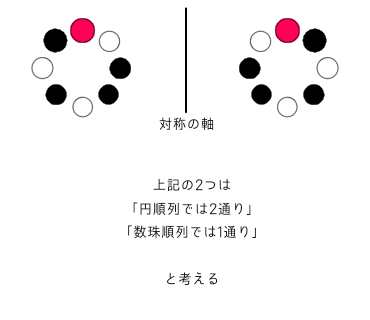
したがって、円順列で計算した答えを2で割ると数珠順列の答えになります

しかし、同じものを含む場合、表裏の区別がない並べ方が存在します

例えば、以下の図のような、もともとの配置が左右対称のものは表裏の区別がありません
数学の問題上ではなく現実の世界でも、以下の図のような配置のネックレスやブレスレットは、誰かがイタズラしてひっくり返しても、その現場を見ていなければ、ひっくり返したことに気づくことは不可能です

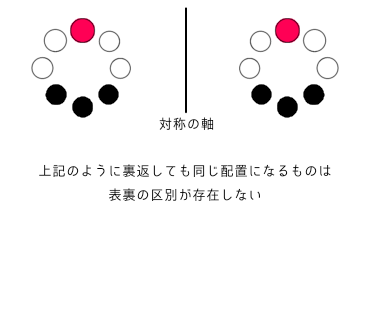
そして、このような表裏の区別が存在しない並び方は、円順列でも数珠順列でも1通りと考えるため、2で割る必要がありません

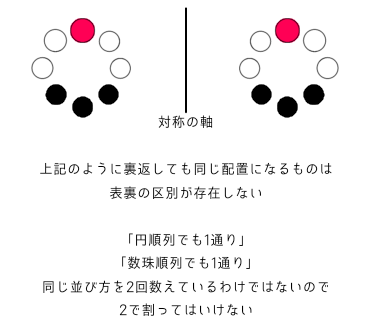
よって、同じものを含む数珠順列では、表裏の区別がない左右対称となっている並び方を除いたものを2で割る必要があります

これが「数珠順列」と「同じものを含む数珠順列」の違いです

この問題は、白玉4個・黒玉3個と同じ色の玉が複数あるため、「同じものを含む数珠順列」で計算します

「同じものを含む数珠順列」は、ただ円順列の答えを2で割ると間違いとなり、左右対称となっている並び方を除いてから2 で割らなければなりません

この問題は、以下の3つの並び方が左右対称となります

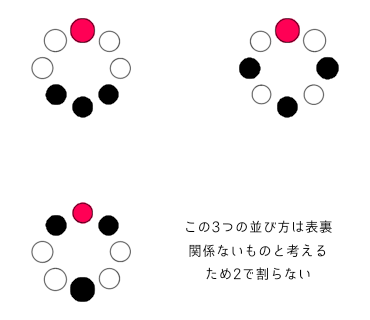
よって計算は以下のようになります

★円順列で計算した全ての並べ方は35通り
★35通りのうち、2で割る必要がない並べ方は3通り
★35通りのうち2で割らなければならない並べ方は32 通り
\begin{align}&3+\frac{32}{2}\\=&3+16\\=&19\end{align}
答え19通り