
この問題はひとつの式の中に\(sin\)と\(cos\)が混在しているので三角関数の合成をして、関数の種類を統一する必要があります
しかし、\(cos\)は\(cos\color{red}{2x}\)、\(sin\)は\(-2sin\color{red}{x}\)となっていて、それぞれの角の大きさが違うため三角関数の合成は使えません
この問題は\(cos2x\)が2倍角になっているので、まず初めに2倍角の公式を使って\(sin\)だけの式に変形してから三角関数の合成を行いましょう
目次
解き方の手順
解き方の手順
①\(sin\) と\(cos\)が混在している式なので、変形して解きやすくする
このとき、\(cos2x\)が2倍角なので、2倍角の公式を使って\(sin\)に統一するとよい
②\(sin\)に統一したあと、\(sinx=t\)と置き換えるとさらに解きやすくなる
③問題の式を\(sinx=t\)と置き換えたら平方完成し、最大値と最小値を見つけやすくする
④最大値と最小値を見つけた後は、\(t\)を\(sinx\)の値に戻す
\(cos2x\)が2倍角なので、2倍角の公式を使って\(sin\)に統一しよう
今回は\(cos\)を\(sin\)に変換するので、\(cos2α=1-2sin^2α\)を使います

変換していこう
\(cos2x\)を\(1-2sin^2x\)に書き換えて式を整理しましょう
\begin{eqnarray}y&=&cos2x-2sinx-1\\y&=&1-2sin^2x-2sinx-1\\y&=&-2sin^2x-2sinx\end{eqnarray}
\(sinx\)を\(t\)に置き換えよう
二次関数が平方完成をすることによって、最大値や最小値がわかるようになっていることを利用して、この問題の最大値と最小値を求めていきます
\(y=-2sin^2x-2sinx\)の\(sinx\)を\(t\)に置き換えると、三角関数の式が二次関数と同じ見た目になるため、わかりやすくなるので必ず置き換えるようにしましょう
\(y=-2sin^2x-2sinx\)の\(sinx\)を\(t\)に置き換えると以下のようになります
\(y=-2t^2-2t\)
\(t\)に置き換えたら平方完成していこう
\(y=-2sin^2x-2sinx\)で\(sinx=t\)とすると\(y=-2t^2-2t\)となります
次はこの\(y=-2t^2-2t\)を平方完成していきます
平方完成の方法を忘れた人はこちらを確認してくださいね
\begin{eqnarray}y&=&-2t^2-2t\\y&=&-2(t^2+t)\\y&=&-2\{(t^2+t+\frac{1}{4})-\frac{1}{4}\}\\y&=&-2(t+\frac{1}{2})^2+\frac{1}{2}\end{eqnarray}
これで平方完成ができたので、つぎはいよいよ最大値と最小値を考えていきます
最大値と最小値を考える前に\(x\)の範囲を再確認しておこう
\(x\)の範囲は\(0≦x≦2π\)、これを\(sin\)の値で表すと\(-1≦sinx≦1\)、また\(sinx=t\)と置き換えているので\(-1≦t≦1\)となります
ここから先は\(-1≦sinx≦1\)ではなく\(-1≦t≦1\)として考えていきます
\(y=-2(t+\frac{1}{2})^2+\frac{1}{2}\)の最大値と最小値を\(-1≦t≦1\)の範囲で考えよう
\(t=-1\)、\(t=1\)を\(y=-2(t+\frac{1}{2})^2+\frac{1}{2}\)に代入して\(y\)の値を求めると最大値・最小値がわかります
ただし、\(y=-2(t+\frac{1}{2})^2+\frac{1}{2}\)は二次関数だから頂点の座標も確認しておかないとミスにつながるので要注意です
代入して計算すると、\(t\)の最小値\(t=-1\)のとき\(y=0\)、頂点の\(t\)座標\(t=-\frac{1}{2}\)のとき\(y=\frac{1}{2}\)、\(t\)の最大値\(t=1\)のとき\(y=-4\)、ゆえに\(y\)の最大値は\(t=-\frac{1}{2}\)のとき\(y=\frac{1}{2}\)、最小値は\(t=1\)のとき\(y=-4\)となる
\(t\)を\(sinx\)に戻そう
最大値と最小値はわかったけれど、まだ答えを書くことはできません
\(sinx\)を\(t\)に置き換えているので元に戻す必要があります
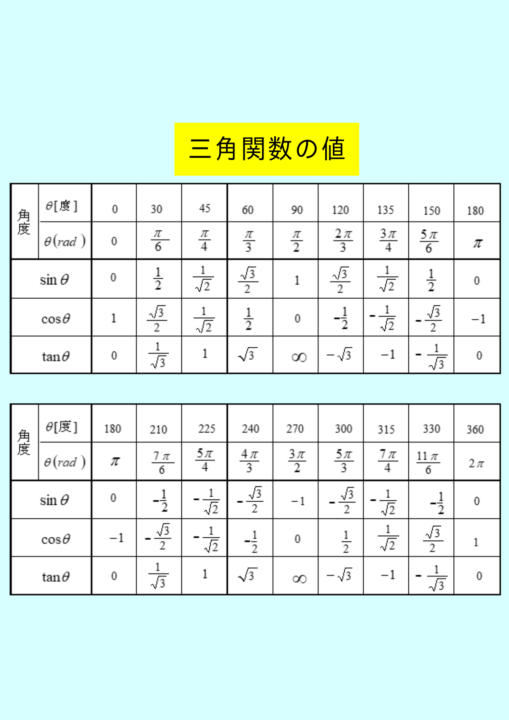
\(t=-\frac{1}{2}\)より\(sinx=-\frac{1}{2}\)、したがって\(x=\frac{7}{6}π、\frac{11}{6}π\)
また\(t=1\)より\(sinx=1\)、したがって\(x=\frac{π}{2}\)
これで最大値・最小値をとるときの\(x\)の値がわかったのであとは答えを書くだけになりました

最大値・最小値をとるときの\(x\)の値がわかったので答えを書こう
最大値・最小値をとるときの\(x\)の値がわかったので\(x\)のとる値と最大値・最小値をしっかりと答えに書いたら完成です
答え
\(\frac{7}{6}π\)、\(\frac{11}{6}π\)のとき最大値\(\frac{1}{2}\)
\(\frac{π}{2}\)のとき最小値\(-4\)