問題を解く手順
①三角関数の合成をする
②最大値と最小値を見つける

まず最初に三角関数の合成をする
1つの式の中に\(sin\)と\(cos\)があるので三角関数の合成を行い、\(sin\)だけの式にすると続きを考えやすくなるよ
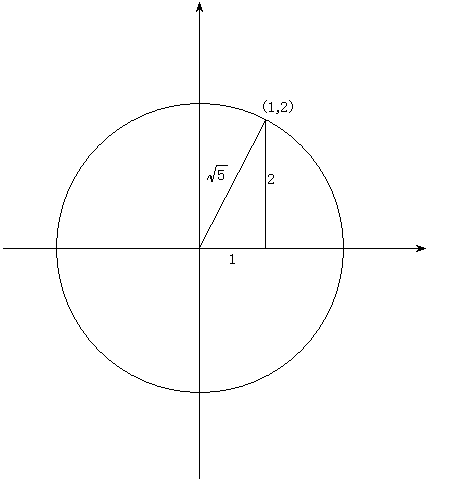
この合成の式に当てはめて計算すると…
\(y=\sqrt{1^2+2^2}sin(θ+α)\)
よって \(y=\sqrt{5}sin(θ+α)\)
ただし、\(sinθ=\frac{2}{\sqrt{5}}\) , \(cosθ=\frac{1}{\sqrt{5}}\)
※この問題のように\(α\)の値がはっきりしないときは\(α\)としたまま考えていこう(\(sin\)と\(cos\)の値は書いておくこと)
合成ができたら最大値と最小値を考えよう
今回の問題のポイントは範囲がないこと
範囲がないということは、\(sin(θ+α)\)はどんな数字でもありえるということ
「範囲が決まっていなければ最大や最小が決まらない」と思うかもしれないが、三角関数の場合は大丈夫
単位円を描いてみると最大値と最小値はすぐにわかるよ
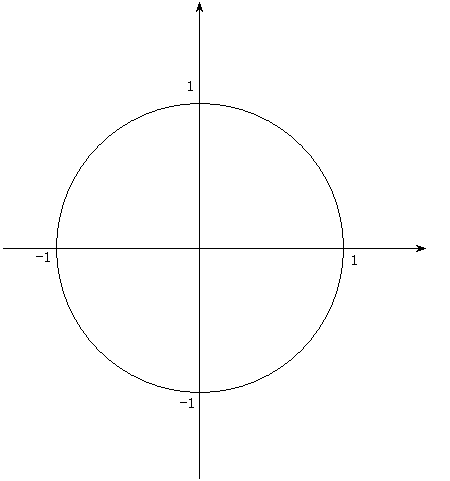
今回の問題は\(\sqrt{5}sin(θ+α)\)なので上の円を\(\sqrt{5}\)倍する
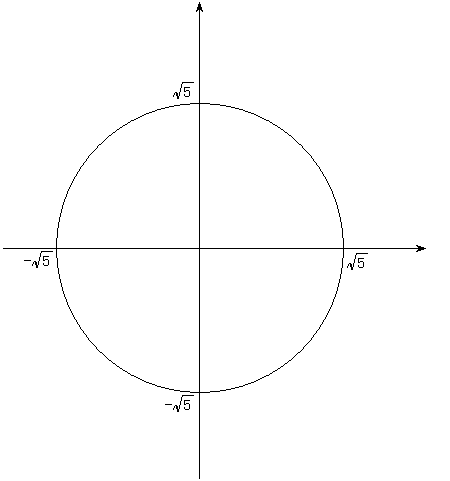
範囲がないので、\(\sqrt{5}sin(θ+α)\)は上の単位円の中のどの値もとることができるということ
したがって、単位円の中から\(y\)の値の最大値と最小値を探すと…
最大値は\(\sqrt{5}\)、最小値は\(-\sqrt{5}\)となる

答え
最後に答えをしっかりと書こう
答え
最大値\(\sqrt{5}\)
最小値\(-\sqrt{5}\)
※範囲が決まっていない三角関数の最大値と最小値のその他の問題はこちら
答えに「\(θ=●\)のとき」(\(θ\)の値)が書かれていないのはナゼ?
今回は問題に範囲の指定がないので、\(y\)の値が最大値・最小値になるときの\(θ\)の値が一つに決まらない
たとえば最大値\(\sqrt{5}\)となるときの\(\sin\)の値は、\(\frac{1}{2}\)かもしれないし\(\frac{5}{2}\)かもしれない
そのため、範囲のない問題のときは、解答欄に最大値と最小値だけ書けばよい
