
この問題を解くためには、まず点Pと点Qの\(x\)座標を\(a\)を用いて表したものが必要になる
Pと点Qの\(x\)座標を\(a\)を用いて表す方法はこちらを確認
問題を解く手順
①PとQの座標を求める
②PとQの座標が座標平面上のどの辺りにあるのか確認する
③\(l\)と\(m\)の傾きをかけ算すると-1なので、△OPQはPO⊥QOの直角三角形になることを確認する
④POとQOの長さを三平方の定理で求める(POとQOが底辺と高さになる)
⑤三角形の面積の公式\(底辺×高さ×\frac{1}{2}\)に当てはめて計算する
点Pと点Qの座標を\(a\)を用いて表すと
P(\(a-\sqrt{1+a^2}\),\(-(a-\sqrt{1+a^2})\))
Q(\(a+\sqrt{1+a^2}\),\((a-\sqrt{1+a^2})\))
※PとQの\(y\)座標は、\(x\)座標を\(a\)を用いて表したあと、Pは\(l\)の式に、Qは\(m\)の式に代入して求めよう
点PとQの座標がわかったけれど、このままでは座標平面上のどこにあるかがわからないので、簡単に確認する。
※だいたいの位置(符号が+か−か)がわからないと、三平方の定理でPOとQOの長さが計算できないのでこの作業は必ず行おう
点Pの位置
\(a^2\)は\(1+a^2\)より小さいので、\(a^2\)<\(1+a^2\)が成り立つ。
これを移項して整理すると、
\(a^2−(1+a^2)\)<0
点Pの\(x\)座標\(a-\sqrt{1+a^2}\)を\(\sqrt{a^2}-\sqrt{1+a^2}\)と変形し、両辺を二乗すると、
\(a^2\)−\(1+a^2\)<0
よって点Pの符号は(−,−(−))→(−,+)
点Qも同様に考えると、点Qの符号は(+,+)
よって△OPQは下のグラフのような直角三角形になる
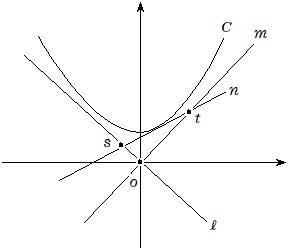
このあと、OPとOQの長さを計算していくが、PとQの座標を\(a\)を用いた形で計算すると計算が大変なので、問題の設定通りPとQそれぞれの\(x\)座標を\(s\)と\(t\)として計算し、後で調整する
OPの長さ
P\((s,−s)\)として三平方の定理に当てはめると
\(OP^2=s^2+(−s)^2\)
\(OP^2=2s^2\)
\(OP=±\sqrt{2}s\)
\(OP=−\sqrt{2}s\)
※sの値がマイナスなので、\(OP=+\sqrt{2}s\)ならば、\(s\)の値を代入するとOPの値がマイナスになるので、不適切
\(OP=−\sqrt{2}s\)に\(s=a-\sqrt{1+a^2}\)を代入したらOPの値となる
\(OP=−\sqrt{2}(a-\sqrt{1+a^2})\)
同様にしてOQも計算する
OQの長さ
Q\((t,t)\)として三平方の定理に当てはめると
\(OQ^2=t^2+t^2\)
\(OQ^2=2t^2\)
\(OQ=±\sqrt{2}t\)
\(OQ=+\sqrt{2}t\)
※tの値がプラスなので、\(OQ=−\sqrt{2}t\)ならば\(t\)の値を代入するとOQの値がマイナスになるので、不適切
\(OQ=+\sqrt{2}t\)に\(t=a+\sqrt{1+a^2}\)を代入したらOQの値となる
\(OQ=\sqrt{2}(a+\sqrt{1+a^2})\)
OPとOQがわかったので、あとは三角形の面積の公式に当てはめて計算すれば答えが求まる
△OPQの面積=\(\frac{1}{2}×OP×OQ\)
△OPQ=\(\frac{1}{2}×\{−\sqrt{2}(a-\sqrt{1+a^2})\}×\{\sqrt{2}(a+\sqrt{1+a^2})\}\)
△OPQ=\(−\frac{1}{2}×\sqrt{2}×\sqrt{2}×(a-\sqrt{1+a^2})(a+\sqrt{1+a^2})\)
△OPQ=\(−\frac{1}{2}×2× \{a^2−(1+a^2)\}\)
△OPQ=\(−(a^2−1−a^2)\)=−(−1)=1
ゆえに、△OPQの面積=1